Red Hot Cyber
La cybersecurity è condivisione. Riconosci il rischio, combattilo, condividi le tue esperienze ed incentiva gli altri a fare meglio di te.
Davide Cavallini : 21 Novembre 2023 07:49
E’ sempre un piacere scrivere articoli per voi. Mi dà ancora più soddisfazione quando vengono letti da persone della nuova generazione, che stanno ancora studiando, oppure da persone che attualmente sono meno incluse in questo settore.
Oggi parleremo della debolezza di alcuni algoritmi di hashing. Avrete certamente sentito – specialmente se state studiando informatica, o siete sviluppatori o sistemisti – che l’algoritmo MD5, ma anche altri algoritmi, come l’SHA1, vengono considerati deboli.
Perché?
La risposta è che possono generare delle collisioni.
La NIS2 è complessa da capire?
Non perdere tempo, segui l'anteprima gratuita del corso che stiamo preparando.Accedi quindi alla nostra Academy e segui l'anteprima del corso della durata di 30 minuti per comprendere i contenuti esclusivi che tratteremo nel corso.per ulteriori informazioni, scrivici ad [email protected] oppure scrivici su Whatsapp al 379 163 8765
Supporta RHC attraverso:
Ma che cosa sono queste collisioni? L’algoritmo MD5 prende come input un dato, che di solito è una stringa o un file. Una volta elaborato l’input, uscirà come risposta un hash di lunghezza fissa di 128 bit, chiamato digest.
Questo è un esempio dell’hash MD5 della parola “password”: 5f4dcc3b5aa765d61d8327deb882cf99
L’algoritmo MD5 è stato sviluppato da Ronald Rivest nel 1991 per sostituire il precedente algoritmo MD4.
Per farla breve l’algoritmo “digerisce” una serie di bit (come una password o un file) che gli passiamo in input, e la “defeca” come output sotto forma di hash con una lunghezza fissa di 128 bit (i bit sono 0 o 1, quindi 2 possibili stati per ogni bit). Infatti MD5 è l’abbreviativo di “Message Digest 5”.
Il risultato ottenuto sarà:
Quindi potremmo ottenere 2 (stati del bit) elevati alla 128 (lunghezza) output diversi. Qui sorge un potenziale problema: siccome gli input possono essere infiniti, ma gli output sono finiti, avremmo più input che output.
Quindi è come avere pochi scatoloni (output) e tanti oggetti da metterci dentro (input). Infatti in questo caso Input > Output (il numero di input è maggiore del numero di output). Ad esempio, se Antonella riempisse con 200 oggetti solo 50 scatoloni, ci sarebbe un’alta probabilità che più oggetti ricadano nello stesso scatolone, e quindi sbatteranno tra di loro, creando una così detta collisione.
La stessa cosa vale anche per l’algoritmo MD5, perché infiniti input sono maggiori di 2 elevato alla 128 output (da ora indicheremo l’elevamento a potenza con il simbolo ^), quindi per forza qualche input diverso ricadrà nello stesso hash.
Quindi possiamo definire barbaramente la collisione come quel fenomeno che avviene quando due oggetti in entrata ricadono in un unico oggetto in uscita. In matematica questo principio è noto come “legge del buco della piccionaia”. Questo è un problema quando parliamo di algoritmi di hashing, in quanto ne compromette la stessa sicurezza.
Una potenziale vulnerabilità in tal senso potrebbe avvenire perchè le password vengono salvate nel database sotto forma di hash, ma facendo i dovuti calcoli probabilistici, come vedremo in seguito è un problema di poco conto nel campo delle collisioni. Invece un problema più importante avviene quando bisogna verificare l’integrità di un file utilizzando l’MD5, cosa che non andrebbe MAI fatta in contesti critici!
Chi sta studiando alle superiori informatica, sicuramente crederà, come lo credevo anche io all’epoca, che la matematica non gli servirà in futuro. Chiunque pensi questo, sappia che però si sta sbagliando di grosso.
Infatti nel nostro campo sapere la matematica è importantissimo in vari settori, a partire dall’intelligenza artificiale, crittografia, quantum computing, ma anche semplicemente per fare un software gestionale che scorpori l’iva o che calcoli le commissioni o tasse.
Ora andremo infatti ad affrontare dal punto di vista matematico il famoso “PROBLEMA DEL COMPLEANNO”. Come abbiamo visto in precedenza, la legge della piccionaia dice che se n articoli vengono messi in m contenitori, con n > m, allora almeno un contenitore dovrà contenere più di un articolo.
Nel pianeta ci sono 7,5 miliardi di persone, ma i giorni nei quali possono compiere gli anni sono solo 365. Questo significa che n persone (7,5 miliardi) possono nascere solo in m contenitori (365 giorni). Chiaramente questo genererà delle collisioni tra compleanni, ovvero più persone compieranno inevitabilmente gli anni lo stesso giorno. Il problema del compleanno è il seguente:
Quante persone devono trovarsi in una stanza affinché la probabilità che due persone condividano lo stesso compleanno sia del 50%, escludendo gli anni bisestili e tenendo conto che la probabilità che una persona nasca in ciascuno dei 365 giorni sia uguale?
Se hai fatto una semplice divisione di 7,5 miliardi per 365, oppure 365 diviso 2, hai risolto male il problema! 🙂 infatti per risolverlo bisogna utilizzare il “calcolo delle probabilità”.
Innanzitutto, indichiamo la probabilità che:
La probabilità dello 0% sarà indicata con il numero 0, e la probabilità del 100% con il numero 1. Analogamente una probabilità del 40% sarà indicata con 0.4, eccetera, cioè il numero percentuale diviso 100.
Siccome la probabilità che due persone compiano gli anni lo stesso giorno, esclude la probabilità che non li compiano lo stesso giorno (in statistica si dice che sono mutualmente esclusive) avremmo che:
P(A) = 1 – P(B)
In questo caso infatti sarebbe più facile sapere la probabilità che non compiano gli anni lo stesso giorno, cioè P(B), per poi ottenere facilmente P(A), facendo una semplice sottrazione.
Quanto è la probabilità che lanciando 2 dadi, esca due volte il numero 6 allo stesso momento?
Siccome il dado è un cubo e quindi ha 6 facce, e solo una faccia contiene il numero 6, la probabilità sarà 1 su 6 per dado.
Dato che lanciamo due dadi allo stesso momento, la probabilità che esca 6 su entrambi i dadi è il PRODOTTO, ovvero l’intersezione delle due probabilità.
Quindi la probabilità che uscirà 6 su entrambi i dadi sarà ⅙ * ⅙ = 1/36
Quindi la probabilità che invece non esca 6 su entrambi i dadi sarà 1 – 1/36 = 35/36
Torniamo quindi al problema del compleanno…
Quindi avremo:
P(B) = 365/365*364/365*363/365 e così via.
Andando avanti per 23 volte otterremo P(B) = 0.492
Quindi se P(A) = 1 – P(B) e quindi P(A) = 1- 0.492, facendo la differenza otterremo P(A) = 0.508
Quindi con 23 persone nella stessa stanza, avremo il 50.8% di probabilità che ci siano due persone che compiono gli anni lo stesso giorno.
Generalizzando possiamo dire che:
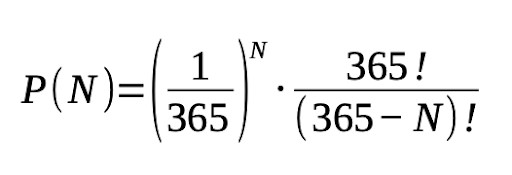
dove N è il numero di persone nella stanza.
Il simbolo ! invece indica il fattoriale, cioè ad esempio se n=3:
Quindi facendo i calcoli avremmo che:
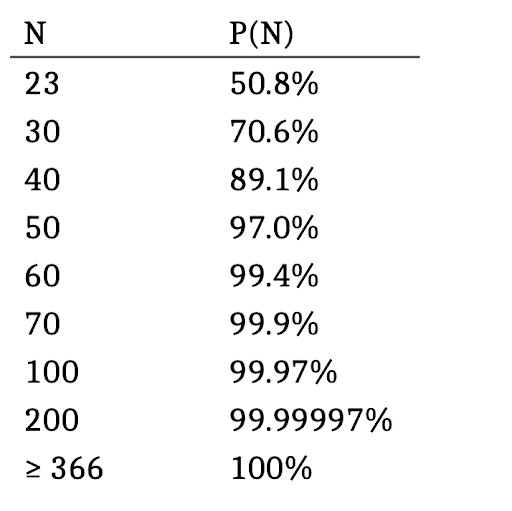
Chiaramente in un gruppo maggiore di 365 persone, che è uguale a dire maggiore o uguale a 366 persone, per il principio della piccionaia, ci sarà il 100% di probabilità di trovare 2 persone con lo stesso compleanno nella stanza.
La stessa formula si può generalizzare come segue per comprendere anche il problema dell’hashing:
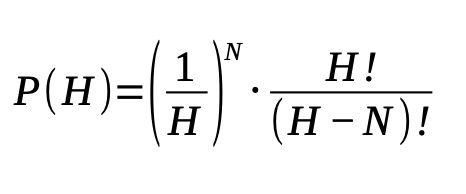
In questo caso H sarà semplicemente lo spazio campionario della funzione di hashing.
Nel caso della funzione MD5, lo spazio campionario sarà come detto prima di 2^128 possibilità.
Risolvendo questa equazione vedrai che una collisione avverrà sempre dopo circa N/2 operazioni, dove N è la dimensione dello spazio campione in bit. Quindi in questo caso dopo dopo circa 2^64 operazioni hai una probabilità del 50% di trovare una collisione. Si tratta di un numero di operazioni molto inferiore rispetto a un attacco di forza bruta.
Quello che vuoi sapere, però, è la possibilità che qualcuno condivida un compleanno (oppure un hash della password o di un file) con te .
Andiamo quindi a proseguire con i calcoli. Innanzitutto esaminiamo la possibilità che qualcuno NON CONDIVIDA il compleanno con te, che chiameremo P(B’), e da questo otterremo P(A’), ovvero la probabilità che qualcuno condivida il compleanno con te.
Supponiamo che tu nasca in un giorno qualsiasi su 365. La seconda persona può nascere in uno qualsiasi degli altri 364 giorni, escluso il tuo compleanno. La terza persona può nascere anche in uno qualsiasi degli altri 364 giorni. E così via, fino all’ennesima persona.
Quindi la possibilità che N persone non condividano il compleanno con te è:
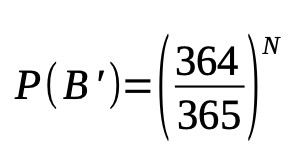
Andiamo ad applicare sempre la stessa formula:
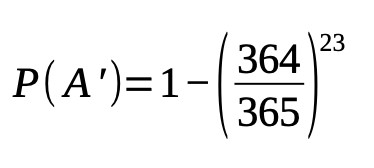
Quindi se nella stanza ci fossero N = 23 persone, avremmo il 6,1% di probabilità che 1 condivida con te il compleanno. Per una probabilità >50% che una persona in una stanza di N persone nasca il tuo stesso giorno, avresti bisogno di 253 persone nella stanza.
Possiamo generalizzare la formula così:
Quindi, qual è la possibilità che un utente malintenzionato possa avere fortuna e trovare una password che abbia lo stesso hash della tua? Dovresti semplicemente prendere P = 0,5 e risolvere per N.
Quindi nel caso dell’MD5 l’attaccante dovrebbe passare attraverso 2^(127,5) hash per avere una probabilità >50% di trovare un hash che collida con il tuo, che è superiore alle 2^127 operazioni teoriche per forzare l’intero spazio campione.
Ciò significa che la probabilità che la password entri in collisione specificamente con la tua è meno probabile rispetto a quella che l’aggressore indovini semplicemente la tua password tra tutte le 2 ^ 128 possibilità.
Inoltre, solo perché qualcuno ha trovato una collisione non significa che sarà in grado di eseguire l’autenticazione: potrebbe essere che la password corrispondente sia lunga 200 caratteri e non sarebbe in grado di inviarla nel campo password perché l’applicazione potrebbe limitare le password a un tot di caratteri.
Quindi diciamo che nel caso delle password, la collisione non rappresenta un particolare problema, perchè è molto più probabile trovare la password con attacchi di forza bruta o con il phising, di cui abbiamo parlato in altri articoli, o con altri tools per costruire dizionari di password mirati.
Invece può diventare molto problematico quando gli aggressori sono in grado di falsificare due file diversi utilizzando lo stesso hash, compromettendone quindi l’integrità.
Un tipico attacco ai file potrebbe essere:
Quindi il mio consiglio è di stare sempre attenti e di utilizzare sempre gli algoritmi consigliati al momento, soprattutto quando si tratta di proteggere delle infrastrutture critiche o che forniscono altre infrastrutture critiche.
Per approfondimenti riguardanti l’ambito della sicurezza delle web applications potete vedere nep sito di OWASP gli articoli sulla Crittographic Failture.
Davide Cavallini