Red Hot Cyber
Sicurezza Informatica, Notizie su Cybercrime e Analisi Vulnerabilità
Nei miei articoli ho cerco spesso di sottolineare il fatto che le competenze di ingegneria del software sono essenziali anche quando si lavora nell’IA, perché alla fine della giornata quello che produciamo è del codice. Lo stesso vale per la teoria algoritmica, perché gli algoritmi di Machine Learning sono pur sempre algoritmi (anche se spesso sono visto come blackbox) e capire come valutarli è essenziale. Ad esempio, sapete come funziona il meccanismo di attenzione nei trasformer?
Quando studiamo o sviluppiamo un algoritmo, è essenziale capire di quali risorse in termini di tempo e spazio ha bisogno. Solo in questo modo possiamo capire come scalerà. Un algoritmo di ordinamento potrebbe sembrare ottimale in un caso semplice in cui dobbiamo ordinare un array di lunghezza n=3, ma potrebbe essere altamente inefficiente quando abbiamo un array di lunghezza n=100.000.
Per questo motivo, non è banale confrontare le prestazioni di due algoritmi diversi. Il primo potrebbe sembrare più veloce in determinati casi e il secondo in altri; abbiamo bisogno di un metodo matematico e formale per valutarli correttamente.
Come abbiamo detto, un algoritmo può comportarsi in modo diverso a seconda dell’istanza in input su cui lavora. Ma allora in quali istanze è giusto monitorare le sue prestazioni? Su quelle in cui è più veloce più lento? Di solito si utilizza il tempo di esecuzione del “worst case”. In questo modo siamo sicuri di cosa accadrà nel caso peggiore. E se il caso peggiore non è così grave, siamo contenti 😊.
Un altro metodo consiste nell’affidarsi alla “aerage case“. In altre parole, creiamo varie istanze di input in modo casuale e facciamo una media dei tempi di esecuzione. Con questo metodo, tuttavia, abbiamo un problema fondamentale: come scegliamo queste istanze casuali?
A causa di questi problemi, preferiamo affidarci allo scenario peggiore.
Se non abbiamo un benchmark, come facciamo a sapere quanto è efficiente un algoritmo che sviluppiamo?
Possiamo iniziare con qualcosa di semplice. Per ogni problema, abbiamo quasi sempre un algoritmo naive (ingenuo) che lo risolve, la forza bruta. Questo consiste nel cercare all’interno dell’intero spazio di ricerca possibile per trovare una soluzione. In breve, le proviamo tutte! Ovviamente, questo è molto inefficiente perché lo spazio di ricerca può essere enorme.
Dobbiamo quindi cercare di formalizzare l’efficienza su un piano matematico su cui possiamo essere d’accordo. Diciamo che un algoritmo è efficiente se ha un tempo di esecuzione polinomiale.
Quindi se esistono due costanti c, d > 0 tali che per ogni istanza di input di lunghezza N il tempo di esecuzione può essere limitato da cN^d passi computazionali (che possono corrispondere, ad esempio, a istruzioni di codice assembly).
Il tempo di esecuzione rimane quindi proporzionalmente lineare rispetto alla dimensione dell’istanza di ingresso.
In informatica, quando esprimiamo il tempo di esecuzione di un algoritmo mediante una funzione, diciamo non consideriamo i termini costanti e di grado minore. Per un tempo di esecuzione del tipo 3,2n²+2n+6 diciamo semplicemente che cresce di un fattore proporzionale a n². Questo perché, su valori grandi di n, il termine più rilevante è n² e quindi questo è sufficiente per avere un’idea della velocità dell’algoritmo.
Supponiamo di avere due funzioni f(n) e g(n).
Diciamo che 𝒇(𝒏) = 𝑶(𝒈(𝒏)) se esiste una costante c > 0, e n_0 > 0 tale che c* g(n) > f(n). Quindi se da un certo punto n_0 in poi g(n) è sempre piu grande di f(n). Intuitivamente, su grandi numeri, f(n) non sarà mai peggiore di g(n).
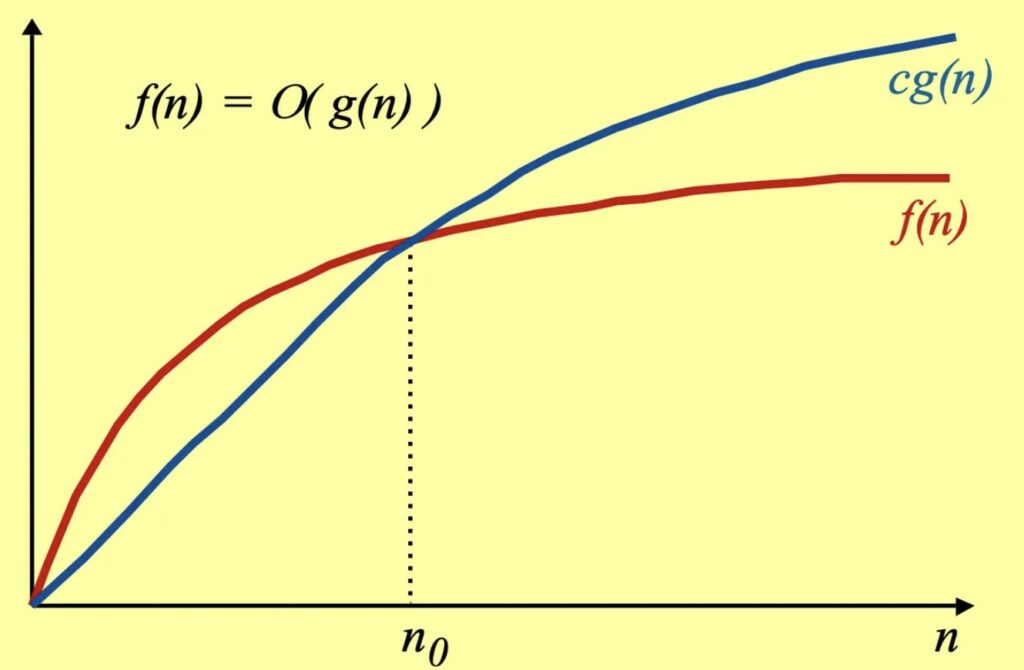
Si dice che𝒇(𝒏) = Ω(𝒈(𝒏)) se esiste una costante c > 0 per cui g(n) da un certo punto in poi (da n_0), g(n) è sempre minore di f(n). Intuitivamente su numeri grandi f(n) sarà sempre più lento di g(n).
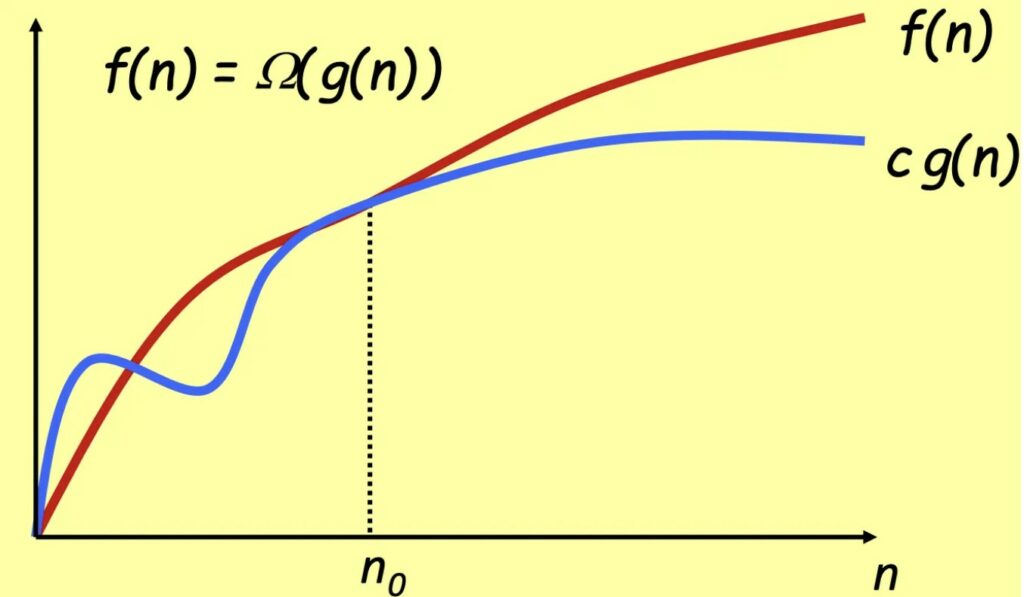
Se f(n) è sia O(g(n)) che Ω(g(n)), allora f(n) cresce proprio come g(n). Allora siamo in grado di trovare due costanti c1 e c2 per le quali vale che c1*g(n) < f(n) < c2*g(n). In questo caso, diciamo che 𝒇(𝒏) = Θ(𝒈(𝒏)).
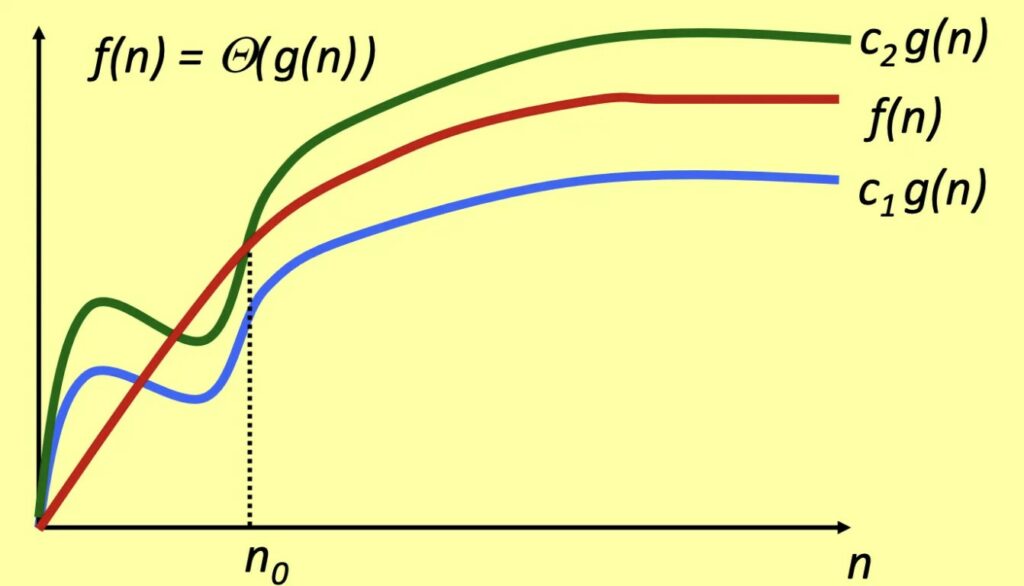
Tra gli algoritmi più comunemente utilizzati, come quelli di ordinamento, ci sono limiti asintotici che ricorrono spesso, come O(n), O(log(n)) e O(n²). Esaminiamone quindi alcuni, in modo da poterne riconoscere i pattern e sapere come distinguerli quando li troviamo nel nostro lavoro.
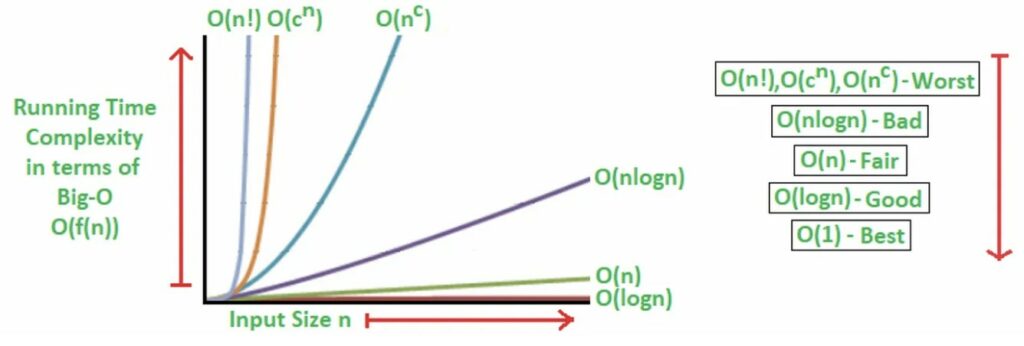
Gli algoritmi di questo tipo hanno un costo di O(n). Ciò significa che per ogni elemento dell’input (immaginiamo l’input come un elenco di n elementi) devono elaborare un numero costante di operazioni. Ad esempio, nel problema di trovare il massimo di una lista, è sufficiente esaminare una volta tutti gli elementi della lista e salvare di volta in volta il più grande, richiedendo così n passi.
Un altro esempio di algoritmo in tempo lineare è quello che esegue il merge di due liste ordinate mantenendo l’ordine.
Qui potete leggere lo pseudocodice dell’algoritmo:
Si tratta di un costo molto comune in informatica. Questo costo è il tempo necessario per creare suddivisioni ricorsive dell’input n, lavorare sulle suddivisioni più piccole create e ricombinare il tutto.
Un esempio classico è mergesort, in cui si divide l’array in parti uguali in modo ricorsivo e ogni volta si ordinano due pezzi alla volta per ricombinare il tutto.
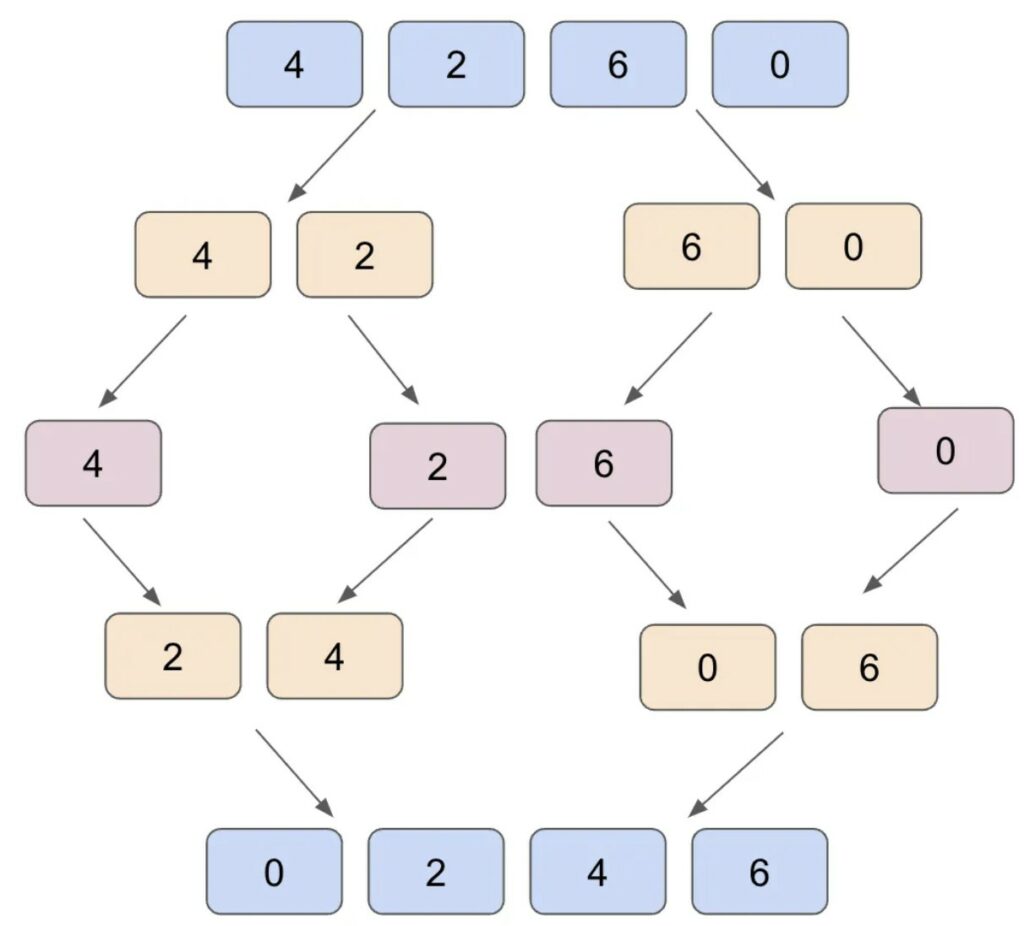
Ecco come implementare il mergesort in Python.
Molti algoritmi hanno un costo computazionale di O(n*log(n)), perché spesso il costo maggiore consiste proprio nell’ordinare un array.
Supponiamo un problema in cui abbiamo n punti sul piano cartesiano. Ogni punto è rappresentato dalle coordinate (x,y). Voglio capire qual è la distanza più breve tra due punti. Un semplice algoritmo potrebbe prendere tutte le coppie di punti, calcolarne la distanza e prendere la coppia con la distanza minima. Ma quanto tempo ci vuole?
Per prendere tutte le coppie possiamo usare il calcolo combinatorio, che ha un costo di O(n²). Invece, possiamo calcolare la distanza tra due punti in modo costante utilizzando una semplice formula. Quindi il costo totale dell’algoritmo è ancora quadratico.
Più pragmaticamente, possiamo dire che incontriamo algoritmi a costo quadratico quando abbiamo due cicli for annidati. In cui scansioniamo un elenco due volte:
In Python:
Sapere come calcolare la complessità temporale (e anche spaziale) di un algoritmo è molto importante. Se un algoritmo è mal concepito, anche il miglior programmatore del mondo non riuscirà a rendere il codice così efficiente da essere utilizzabile.
Esistono tecniche che ci permettono di convertire la complessità temporale in complessità spaziale, come la programmazione dinamica, che vedremo nel prossimo articolo. Possiamo anche avere dei compromessi, sviluppando algoritmi che diano un risultato corretto con una certa probabilità ma che siano più veloci.
Inoltre, quando si tratta di colloqui, questo è uno degli argomenti più importanti da conoscere!Spero che questo articolo vi abbia aiutato in qualche modo a farvi un’idea di questo vasto mondo!
Ti è piaciuto questo articolo? Ne stiamo discutendo nella nostra Community su LinkedIn, Facebook e Instagram. Seguici anche su Google News, per ricevere aggiornamenti quotidiani sulla sicurezza informatica o Scrivici se desideri segnalarci notizie, approfondimenti o contributi da pubblicare.
Innovazione
Cybercrime
Vulnerabilità
Innovazione
Cyber Italia