Roberto Campagnola : 6 Gennaio 2022 20:10
Autore: Roberto Campagnola
Data Pubblicazione: 5/12/2021
La definizione di algoritmo è di per sé semplice: una serie di operazioni da compiere in un preciso ordine per eseguire un’azione o risolvere un problema. Tutti noi abbiamo familiarità con il concetto di algoritmo, anche se non matematicamente e formalmente precisa, a vari livelli: li abbiamo imparati alle elementari per calcolare le operazioni in colonna, li esaminiamo ogni volta che dobbiamo preparare una ricetta, o per trattare dati mediante machine learning.
PARTE LA PROMO ESTATE -40%
RedHotCyber Academy lancia una promozione esclusiva e a tempo limitato per chi vuole investire nella propria crescita professionale nel mondo della tecnologia e della cybersecurity!
Approfitta del 40% di sconto sull’acquisto congiunto di 3 corsi da te scelti dalla nostra Academy. Ad esempio potresti fare un percorso formativo includendo Cyber Threat intelligence + NIS2 + Criptovalute con lo sconto del 40%. Tutto questo lo potrai fruire, dove e quando vuoi e con la massima flessibilità, grazie a lezioni di massimo 30 minuti ciascuna.
Contattaci tramite WhatsApp al 375 593 1011 per richiedere ulteriori informazioni oppure scriviti alla casella di posta [email protected]
Supporta RHC attraverso:
Ti piacciono gli articoli di Red Hot Cyber? Non aspettare oltre, iscriviti alla newsletter settimanale per non perdere nessun articolo.
A livello informatico, tutti gli algoritmi richiedono energia, tempo e potenza di calcolo per compiere le operazioni, ma non sono tutti equivalenti anche se il risultato può essere uguale.
Per creare una classificazione degli algoritmi, per identificare quale può essere più conveniente da usare per risolvere un problema si ricorre al concetto di complessità di un algoritmo, definita come la quantità di tempo o il numero di operazioni necessarie per elaborare dati di un registro di dimensione N.
Alcuni algoritmi, tra i più efficienti, hanno una complessità polinomiale, cioè il numero di operazioni necessarie per arrivare al risultato cresce come una qualunque potenza di N, numero di bit che stiamo elaborando. Altri algoritmi, molto meno efficienti, hanno una complessità che cresce esponenzialmente con il numero di bit, per esempio 2ⁿ eⁿ etc.
Gli algoritmi quantistici, implementati agendo sui qubit caratterizzati da differenti tecnologie di costruzione (superconducting qubit, ion trap, quantum dot etc), hanno alla base una matematica piuttosto complicata e, sfruttando la sovrapposizione coerente di stati, portano ad una riduzione di complessità davvero straordinaria e quindi a possibili prestazioni senza precedenti. Qui esporremo i due algoritmi più famosi: l’algoritmo di Grover e l’algoritmo di Shor. E’ interessante notare che entrambi questi algoritmi sono stati ideati rispettivamente nel 1996 e nel 1994, ben prima della realizzazione pratica del primo quantum computer.
Nel 1996 Lov Grover, ideò un algoritmo quantistico di ricerca che si proponeva di trovare una risposta al seguente problema: dato uno spazio di ricerca di dimensione N, di cui non conosciamo la struttura dell’informazione in esso contenuta, vogliamo trovare un elemento di tale spazio con precise proprietà.
Adoperando le tecniche della computazione e della teoria dell’informazione classica, il numero di operazioni necessarie per risolvere il problema è di ordine N, pari quindi alla dimensione del “database” che stiamo esaminando.
L’algoritmo di Grover consiste nella ripetizione di alcune subroutine quantistiche e grazie alle proprietà della meccanica quantistica e anche (ma questo non sorprende affatto) una trattazione matematica piuttosto complicata e solo apparentemente “magica” (una delle subroutine dell’algoritmo è chiamata “Oracolo”), riesce a risolvere il problema con un numero di operazioni che è ordine
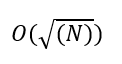
Bisogna notare che nel caso di N molto grande, l’operazione di radice quadrata riduce la complessità in maniera notevole.
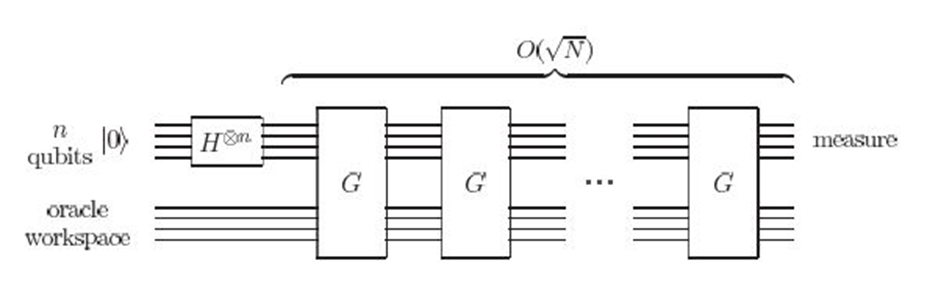
Rappresentazione schematica dell’algoritmo di ricerca, con la trasformata di Hadamard per la sovrapposizione di stati, e le subroutine G dell’algoritmo di Grover
L’algoritmo ideato da Peter Shor, professore di matematica applicata al MIT, nel 1994 ha lo scopo di scomporre i numeri interi in numeri primi, un problema che ha applicazioni in molteplici campi ed è di straordinaria importanza in ambito matematico, e sappiamo che
“L’universo è scritto in lingua matematica, e i caratteri son triangoli, cerchi, ed altre figure geometriche, senza i quali mezzi è impossibile a intenderne umanamente parola“
L’algoritmo di Shor si basa sulla Trasformata di Fourier quantistica (QFT, Quantum Fourier Transform) una trasformazione lineare che è l’analogo quantistico della trasformata di Fourier classica. Quest’ultima è una legge che trasforma una funzione in una altra, permettendo di scrivere una funzione dipendente dal tempo come combinazione lineare di funzioni esponenziali. L’operatore classico da cui si parte è un tipo di trasformata di Fourier, la Trasformata Discreta di Fourier (DFT, Discrete Fourier Transform) usata in numerosissimi ambiti (elaborazione di immagini, elaborazioni di segnali, meccanica dei fluidi, risoluzione di complesse equazioni differenziali alle derivate parziali, etc); applicando la DFT ad uno spazio di Hilbert n-dimensionale proprio della meccanica quantistica ne troviamo l’analogo quantistico: la QFT.
Tale funzione può essere implementata mediante gate quantistici tra cui i gate di Hadamard, di cui abbiamo già parlato nel numero di scorso, e i gate di phase estimation.
L’algoritmo di Shor si compone di due fasi: una fase che può essere eseguita su un calcolatore classico, che ha lo scopo di trasformare la fattorizzazione in numeri primi nel processo di individuazione del periodo di una opportuna funzione, e una parte quantistica che, grazie alla sovrapposizione coerente di stati dei qubit, riesce a trovare il periodo della funzione.
La fase quantistica è quella che porta alla riduzione della complessità generale del processo e alla diminuzione del tempo necessario per raggiungere lo scopo: attualmente, infatti, l’algoritmo classico più efficiente per la fattorizzazione in numeri primi è il Crivello generale dei campi numerici e ha una complessità esponenziale nel numero di cifre del numero da fattorizzare, O(eⁿ) mentre l’algoritmo di Shor ha una complessità polinomiale nel logN., quindi notevolmente minore!
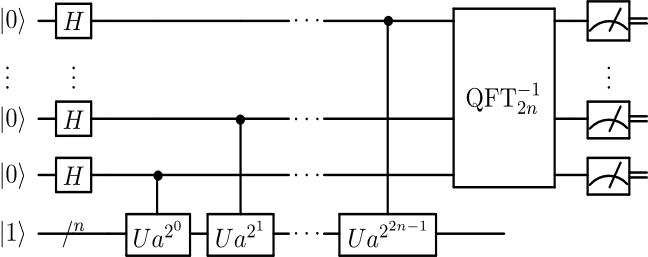
Rappresentazione della subroutine quantistica dell’algoritmo di Shor
Entrambi gli algoritmi descritti sono probabilistici e non deterministici, quindi forniscono il risultato corretto “con alta probabilità” ma comunque minore di 1, problema che in parte si risolve aumentando le iterazioni dell’algoritmo. Inoltre, connessa al problema e alla formulazione degli algoritmi, si apre la questione di quanto e come un computer quantistico possa simulare processi fisici.
Sappiamo che la natura è di per se’ quantistica, e ogni volta che tentiamo di risolvere problemi elementari con un computer classico (simulare urti tra particelle, descrivere il moto di atomo in un gas, le interazioni tra proteine in un organismo) stiamo solo fornendo alla macchina una nostra approssimazione della realtà, sicuramente più corretta possibile ma pur sempre una approssimazione.
Programmato nel modo corretto, un computer quantistico potrebbe descrivere e replicare esattamente il processo oggetto di studio, perché attraverso i qubit sta utilizzando fenomeni quantistici, e non una approssimazione della realtà. Questo tema lo affronteremo anche nella prossima “lezione” in cui cercheremo di capire quali sono i possibili ostacoli al processo di computazione quantistica.
Credit:
Quantum Computation and Quantum Information – Nielsen & Chuang
Image credit: https://en.wikipedia.org/wiki/Shor%27s_algorithm
Roberto Campagnola“Combattere il cybercrime è come estirpare le erbacce: se non elimini le radici a fondo, queste ricresceranno” e oggi, più che mai, questa verità si conferma ess...
Immagina di aprire, come ogni sera, il bookmark del tuo forum preferito per scovare nuove varianti di stealer o l’ennesimo pacchetto di credenziali fresche di breach. Invece della solita bachec...
Il 22 luglio 2025, Mozilla ha rilasciato Firefox 141, un aggiornamento volto a migliorare la sicurezza del browser. Nell’ambito del Bollettino MFSA 2025-56, sono state risolte 18 vulnerabilit&#...
Secondo gli esperti di sicurezza informatica, diversi gruppi di hacker cinesi stanno sfruttando una serie di vulnerabilità zero-day in Microsoft SharePoint nei loro attacchi. In particolare, ...
Un attacco informatico di vasta portata ha violato la National Nuclear Security Administration (NNSA) degli Stati Uniti attraverso il software per documenti Sharepoint di Microsoft, ha confermato...
Iscriviti alla newsletter settimanale di Red Hot Cyber per restare sempre aggiornato sulle ultime novità in cybersecurity e tecnologia digitale.
Copyright @ REDHOTCYBER Srl
PIVA 17898011006
