Red Hot Cyber
La cybersecurity è condivisione.
Riconosci il rischio, combattilo, condividi le tue esperienze ed
incentiva gli altri a fare meglio di te.
Menu
La cybersecurity è condivisione.
Riconosci il rischio, combattilo, condividi le tue esperienze ed
incentiva gli altri a fare meglio di te.
Antonio Piovesan : 28 Settembre 2021 11:34
Gran Bretagna, decenni centrali del XIX secolo, tempi di ambizioni ingegneristiche senza precedenti.
Ingegneria, trasporti, comunicazioni, architettura, scienza e manifattura sono in uno stato evolutivo febbrile. Inventori e ingegneri sfruttano nuovi materiali e nuovi processi: sembra non esserci fine all’invenzione e all’innovazione.
I motori a vapore lentamente sostituiscono gli animali come fonte di forza motrice. Le navi di ferro iniziano a competere con la vela, le reti ferroviarie si espandono rapidamente e il telegrafo elettrico inizia a rivoluzionare le comunicazioni. La scienza, l’ingegneria e le nuove tecnologie fiorenti garantiscono illimitate innovazioni.
Supporta Red Hot Cyber attraverso
Ingegneri, architetti, matematici, astronomi, banchieri, attuari, operai, agenti di assicurazione, statistici, navigatori, chiunque abbia bisogno di calcoli, si affida a tavole numeriche stampate per qualcosa di più che semplici calcoli.
Le tabelle stampate vengono calcolate, copiate, controllate ma composte a mano, ma .. “Errare humanum est” .. gli esseri umani sono notoriamente inclini di natura all’errore e alcuni temono che gli errori non rilevati in una stampa siano possibile fonte di disastri economici o di altra natura.
Raccontiamo in questo articolo la storia di un’idea, la storia di una coppia di precursori dei propri tempi, delle origini del calcolo automatico o, come da titolo di un testo a me caro di Silvio Hénin, parliamo de “Il computer dimenticato”.
Ma chi sono i protagonisti di questa storia?
Matematico inglese (Totnes, Devonshire, 1791 – Londra 1871), noto specialmente per studi e progetti relativi a macchine calcolatrici automatiche, tra i quali quello della “macchina analitica” (analytical engine).
Dal 1828 al 1839, è Professore lucasiano di matematica, termine usato per identificare il titolare della cattedra di matematica (Lucasian Chair of Mathematics) all’Università di Cambridge, in Inghilterra. Sono stati professori Lucasiani (tra gli altri) nomi molto noti della Fisica:
Vista l’importanza delle tavole matematiche nella sua epoca (come detto per l’economia, la navigazione, il commercio et altro) e soprattutto visto l’alto numero di errori di calcolo presenti in queste tavole, Babbage pensa (è un’idea nata nel 1812) di trovare un metodo grazie al quale le tavole matematiche possano essere calcolate da una macchina, non soggetta agli errori, alla stanchezza e alla noia in cui possono incorrere gli esseri umani pagati per fare i calcoli manualmente (fino alla prima metà circa del XX secolo, “computer” era il termine inglese per indicare un essere umano pagato per far di conto, per effettuare calcoli).
Babbage è affascinato dal lavoro sulle macchine per il calcolo di Blaise Pascal e Gottfried Leibniz (calcolatrice di Leibniz, in inglese Stepped Reckoner), ha grande familiarità con le tavole logaritmiche ed ha una profonda avversione per il disordine.
Babbage si interessa anche di crittografia/crittoanalisi: realizza (per scommessa forse?) un metodo per la “violare” le cifrature effettuate con il cifrario di Vigenère, un sistema “polialfabetico” allora chiamato “la cifratura indecifrabile” (La chiffre indéchiffrable), attribuito al francese Blaise de Vigenère (1523 – 1596). Tuttavia, egli non pubblicherà mai la sua scoperta (pare forse perché secretata dal governo del Regno Unito, che preferiva mantenere il vantaggio dato dalla possibilità di decifrare senza che chi cifrava sapesse della possibilità di leggere il testo in chiaro), che risale probabilmente al 1854 e che gli verrà attribuita solo nel XX secolo in base all’esame dei suoi appunti.
Augusta Ada King Byron, contessa di Lovelace (10 dicembre 1815 – 27 novembre 1852) – matematica e scrittrice inglese, nota principalmente per il suo lavoro sul “computer meccanico generico” proposto da Charles Babbage, la macchina analitica.
Ada Byron è l’unica figlia legittima del poeta Lord Byron e della matematica Anne Isabella Noel Byron. Tutti gli altri figli di Byron nascono invece fuori dal matrimonio, da altre donne. Byron si separa dalla moglie un mese dopo la nascita di Ada e lascia l’Inghilterra per sempre quattro mesi dopo. Byron commemora la separazione dalla figlia in una poesia il cui inizio recita:
“La tua faccia è come quella di tua madre, la mia bella bambina! ADA! Figlia unica della mia casa e del mio cuore?”.
Il padre di Ada muore in Grecia quando Ada ha solo otto anni. Anne Isabella promuove l’interesse di Ada per la matematica e la logica nel tentativo di impedirle di sviluppare la pazzia e le inclinazioni percepite nel padre. Nonostante ciò, Ada rimane interessata a padre, chiamando i suoi due figli Byron e Gordon. Alla sua morte, Ada viene sepolta accanto al padre su sua richiesta. Sebbene spesso malata durante l’infanzia, Ada prosegue gli studi in modo assiduo e con continuità.
Ada sposa William King nel 1835: King viene nominato conte di Lovelace nel 1838, Ada quindi diventa così contessa di Lovelace.
Le sue imprese educative e sociali la portano in contatto con scienziati come Andrew Crosse, Charles Babbage, Sir David Brewster, Charles Wheatstone, Michael Faraday e l’autore Charles Dickens, contatti che durante la sua vita sfrutta per approfondire la sua istruzione.
Ada descrive il suo approccio al sapere come “scienza poetica” e definisce sé stessa “Analista (e metafisica)”
La prima macchina diBabbage, la macchina alle differenze (“Difference Engine No. 1”), fu progettata per calcolare e tabulare automaticamente funzioni matematiche chiamate polinomi (sviluppi in serie di Taylor) che hanno importantissime applicazioni generali in matematica e ingegneria. Babbage lavorò a stretto contatto con Joseph Clement, un maestro attrezzista e disegnatore incaricato di realizzarne le parti meccaniche.
Un ritratto di Charles Babbage
Babbage presentò il modello di quella che lui chiamò macchina alle differenze (Difference Engine) alla Royal Astronomical Society il 14 giugno 1823 in un lavoro intitolato “Note on the application of machinery to the computation of astronomical and mathematical tables“.
La prima macchina alle differenze richiedeva 25.000 parti e avrebbe avuto un peso di circa quattro tonnellate.
Replica moderna del modello di macchina alle differenze n. 1 creato nel 1832 da Babbage
La costruzione fu bruscamente interrotta nel 1833 quando Clement abbatté gli attrezzi e licenziò i suoi operai a seguito di una disputa con Babbage sul risarcimento per aver spostato l’officina di Clement più vicino alla casa di Babbage.
La macchina non è mai stata costruita: circa 12.000 parti di precisione inutilizzate sono state successivamente fuse come rottami. Per il governo britannico che aveva finanziato l’impresa, il progetto fu un costoso fallimento. Quando furono pagati i conti finali, il Tesoro aveva speso 17’500 sterline – equivalenti al costo di ventidue locomotive a vapore costruite dalla fabbrica di Robert Stephenson nel 1831 – una somma enorme.
Parte della macchina differenziale di Babbage, assemblata dopo la sua morte dal figlio, utilizzando parti trovate nel suo laboratorio
Dettaglio della replica del modello di macchina alle differenze n. 1 creato nel 1832
Ma cerchiamo di capire perché si parla di differenze, di macchina alle differenze.
Il metodo delle differenze costanti
Per calcolare i valori di funzioni trigonometriche o logaritmiche si può usare un metodo basato sugli studi/sulle scoperte del matematico Brook Taylor.
Taylor ha dimostrato che ogni funzione matematica (seno, coseno, tangente, logaritmo eccetera) può essere approssimata da un polinomio della forma:
ax⁶ + bx⁵ + cx⁴ + dx³ + ex² + fx + g
Più è alto l’ordine del polinomio (cioè maggiore è il più grande esponente di x) più l’approssimazione sarà accurata/precisa. Ma cosa c’entra ciò con le figure di ruote dentate viste in precedenza? Come possiamo usare uno strumento puramente meccanico, la macchina alle differenze, fatta “ruotare” o meglio “azionata” da una manovella manuale per effettuare calcoli?
Vediamolo con un esempio.
Ipotizziamo che la funzione matematica che “ci serve”, di cui vogliamo cioè calcolare i valori, sia approssimabile con il polinomio
y = x² + 2x + 3
Calcoliamo per valori crescenti x da 1 a 6 il valore di y
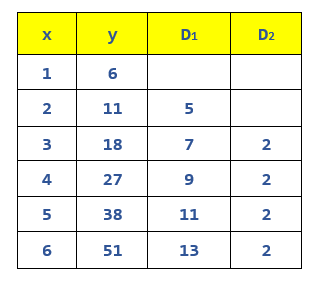
Per i valori da 1 a 6 di x abbiamo calcolato i valori della colonna y; nella colonna D1 abbiamo calcolato la differenza tra un valore di y ed il precedente; nella colonna D2 abbiamo calcolato la differenza tra un valore di D1 ed il precedente.
Si può notare che per il polinomio di ordine 2 (la X con esponente più alto è elevata alla seconda) la seconda differenza da un valore sempre costante…. Per un polinomio di ordine 6, ad esempio, la tabella del nostro esempio avrebbe 8 colonne: la colonna x, la colonna y seguite da 6 colonne D1 D2 D3 D4 D5 D6.
Usando la tabella precedente possiamo calcolare i valori del polinomio non calcolando una moltiplicazione (x moltiplicato per se stesso) seguita da due addizioni, ma solo addizioni … Esempio:
X = 7D2 = 2D1 = 15Y = 15 + 51 = 66Verifica: 66 = 7² + (7 x 2) + 3 = 49 + 14 + 3 = 49 + 17 = 66X = 8D2 = 2D1 = 17Y = 17 + 66 = 83Verifica: 83 = 8² + (8 x 2) + 3 = 64 + 16 + 3 = 64 + 19 = 83
Babbage era conoscenza, come detto, degli studi di Taylor, quindi, progettò una macchina che potesse sfruttare il procedimento appena descritto, capace di trasformare il calcolo approssimato ad esempio di valori di funzioni logaritmiche o trigonometriche in semplici somme. Chi calcolava avrebbe dovuto solo girare una manovella e ad ogni scatto della manovella sarebbe stato calcolato un nuovo valore successivo della variabile y.
Il progetto di Babbage prevedeva le 7 colonne y D1 D2 D3 D4 D5 D6 rappresentate su 7 colonne di ruote dentate: ogni ruota era divisa un 10 settori (da 0 a 9) e ogni colonna aveva 6 ruote per poter rappresentare i numeri a 0 a 999’999. Le ruote di ogni colonna ingranavano con le corrispondenti ruote dell’altra per poter riportare le somme dalla colonna D6 alla D5, dalla D5 alla D4 e così via fino alla colonna finale y. Un meccanismo ad hoc garantiva di tener conto dei riporti quando la somma avesse superato il valore 10.
Una successiva idea di Babbage fu quella di dotare la macchina alle differenze di stampante, per non dover annotare di volta in volta a mano i valori calcolati per la variabile y.
Nel 1834, con il progetto della macchina alle differenze n.1 bloccato per mancanza di finanziamenti dal governo, Babbage concepì una nuova macchina, più ambiziosa, in seguito chiamata Macchina analitica (Analytical Engine), una macchina “informatica” programmabile per tutti gli usi. La macchina analitica può essere pensata come un “salto di qualità” a livello logico e il suo design può essere visto come uno dei più sorprendenti successi intellettuali del XIX secolo.
La macchina analitica presentava molti principi essenziali che si trovano nei moderni computer digitali e la sua concezione segna il passaggio dall’aritmetica meccanizzata (le macchine di Pascal e Leibniz) al calcolo generale completo. Babbage può essere considerato ‘il primo pioniere dei computer’ o del calcolo automatico programmabile per questo suo progetto mai realizzato in concreto.
“ … The drawings of the Analytical Engine have been made entirely at my own cost: I instituted a long series of experiments for the purpose of reducing the expense of its construction to limits which might be within the means I could myself afford to supply. I am now resigned to the necessity of abstaining from its construction… ”
La macchina analitica aveva molte caratteristiche essenziali che si trovano nel moderno computer digitale. Era programmabile utilizzando schede perforate, un’idea presa in prestito dal telaio Jacquard utilizzato per la tessitura di motivi complessi nei tessuti; aveva un “Negozio” (Store) dove potevano essere conservati numeri e risultati intermedi ed un “Mulino” (Mill) separato dove veniva eseguita l’elaborazione aritmetica. Aveva un repertorio interno delle quattro funzioni aritmetiche e poteva eseguire direttamente moltiplicazioni e divisioni. Era anche capace di funzioni per le quali abbiamo i nomi moderni di salto condizionale/if, switch, loop (iterazione) sebbene Babbage non usasse mai questi termini.
La macchina aveva una varietà di output tra cui stampa cartacea, le schede perforate, plottaggio grafico e la produzione automatica di stereotipi (vassoi di materiale morbido in cui venivano impressi i risultati che potevano essere usati come stampi per realizzare lastre da stampa).
Schede perforate
La struttura logica dello “Engine analitico” era essenzialmente la stessa di quella che ha dominato la progettazione dei computer nell’era elettronica: la separazione della memoria (il “Negozio/Store”) dal processore centrale (il “Mulino/Mill”), l’operazione seriale mediante un ciclo iterativo di esecuzione di calcoli e strutture per l’immissione e l’emissione di dati e istruzioni.
“The Analytical Engine weaves algebraic patterns just as the Jacquard loom weaves flowers and leaves.”
Nel 1833 Babbage incontrò Ada Lovelace, figlia del ben noto poeta britannico Lord Byron, a una festa. Lovelace, appena diciassettenne, aveva una formazione matematica che era insolita per una donna a quel tempo. Ada rimase incantata dal lavoro di Babbage sulle macchine per il calcolo e col tempo divenne un’entusiasta sostenitrice di Babbage.
Modello di macchina analitica
Babbage visitò Torino nel 1840 per partecipare, presso l’Accademia delle Scienze, al secondo Congresso degli scienziati italiani. Discusse le sue idee con matematici italiani, tra cui Luigi Menabrea. Durante la visita di Babbage, Menabrea raccolse tutto il materiale necessario per descrivere la macchina analitica e lo pubblicò nell’ottobre 1842 in Francia in lingua francese.
L’idea del salto condizionato, la capacità di cambiare la sequenza delle operazioni automaticamente in base al risultato numerico intermedio ottenuto in un particolare momento dalla macchina analitica, fu proprio frutto di una conversazione avvenuta a Torino tra Babbage ed il matematico Ottaviano Fabrizio Mossotti.
Nel 1843 Ada Lovelace pubblicò l’articolo dell’ingegnere italiano Menabrea tradotto dal francese in inglese. In esso aggiunse ampie note sue proprie che resero l’articolo in versione inglese tre volte più lungo dell’articolo originale francese. Le note includevano una descrizione dei passaggi che il “motore analitico” avrebbe intrapreso per risolvere alcuni problemi matematici – procedure che ora chiameremmo programmi – le prime descrizioni pubblicate del genere (facciamo riferimento alla nota G – il calcolo dei numeri di Bernoulli).
La Lovelace ipotizzò che la macchina potesse andare oltre i numeri e più in generale manipolare i simboli secondo le regole. “Vide” che i numeri potevano rappresentare entità diverse da mere quantità… lettere dell’alfabeto … note musicali … e che manipolando i numeri, le macchine di calcolo potevano estendere i loro poteri oltre il mondo della matematica. Alla luce degli sviluppi nel XX secolo, questa nozione può sembrare profetica: Babbage pare non sia arrivato ad immaginare ciò con chiarezza, molto probabilmente non aveva compreso le potenzialità del suo progetto.
Ada fu una delle poche persone a capire pienamente le idee di Babbage: vi sono, in effetti, indizi (monografia di Menabrea) dove probabilmente Ada suggerisce l’uso di schede perforate del Telaio Jacquard per la macchina analitica progettata da Babbage.
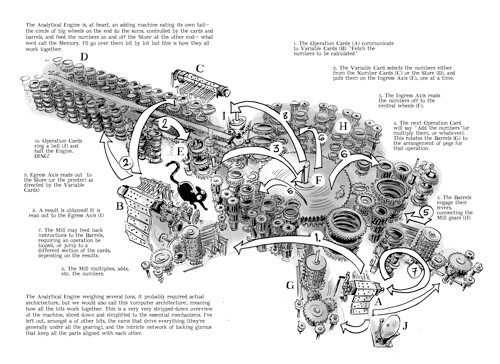
Abbiamo parlato di Mill (unità antiemetica), di Store (unità di memoria) e schede perforate “prese a prestito” dal telaio Jacquard: vediamo come ciò si basa e costituisce un salto evolutivo logico della macchina alle differenze n.1.
Esistevano quattro tipologie di schede perforate:
Le schede lette in sequenza dalla macchina ne permettevano la programmabilità.
Se volessimo calcolare usando la macchina analitica il valore y della seguente equazione
Y = 34 * (27 + 9) / 12
I numeri 34, 27, 9 e 12 dovrebbero venire registrati in 4 colonne dello Store siano esse V1 V2 V3 e V4.
A tal fine usiamo quattro schede dei numeri. Le colonne V5 V6 e V7 servirebbero per i risultati intermedi e per il risultato finale:
Altre schede sarebbero necessarie per condurre la attività di stampa finale del risultato.
Esempi molto più complessi si possono trovare nell’articolo di Menabrea tradotto da Ada Lovelace in inglese.
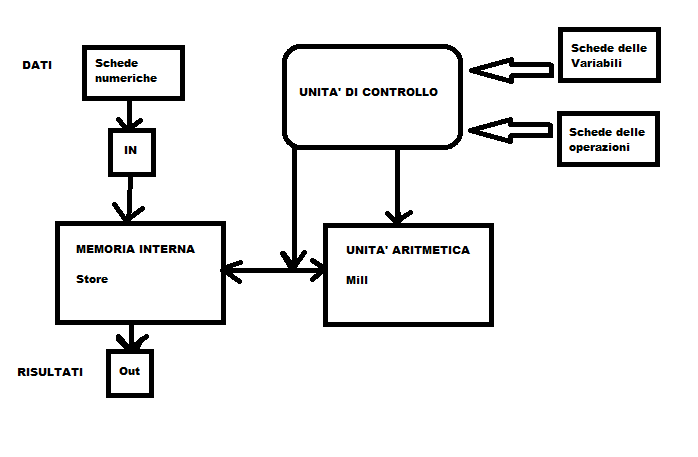
Architettura di Babbage (Macchina analitica)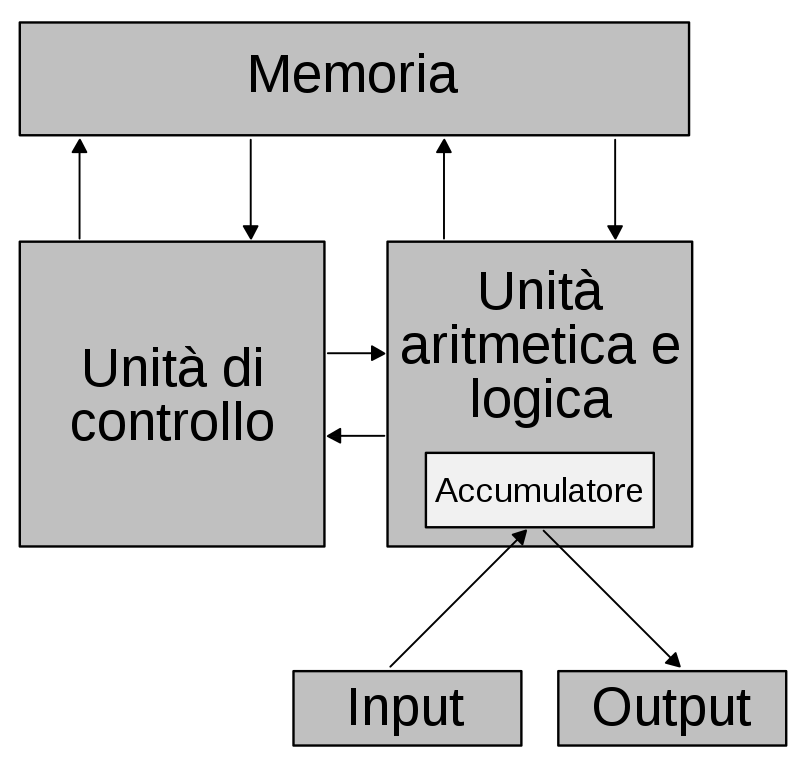
Architettura di Von Nuemann : in Von Neumann “input” è costituito sia dai DATI che dal PROGRAMMA
Mentre Babbage perfezionava i meccanismi della macchina analitica, cercava anche di vedere come avrebbe potuto semplificare il design della macchina delle differenze. Tra il 1847 e il 1849 progettò una nuova macchina, il Difference Engine No. 2. Il nuovo design beneficiò di molte delle tecniche sviluppate per la più esigente macchina analitica.
Il nuovo design era elegante ed efficiente e richiedeva un terzo del numero di parti della macchina alle differenze n. 1 per una maggiore potenza di calcolo. Con 8.000 parti, la macchina sarebbe pesata cinque tonnellate e avrebbe misurato undici piedi di lunghezza e sette piedi di altezza. Babbage non fece alcun tentativo di costruire tale macchina. Questo è il progetto che è stato in effetti costruito e completato nel 2002, ed è il primo dei progetti di macchine di Babbage ad essere stato realizzato nella sua interezza.
Seconda macchina differenze
Babbage non riuscì a costruire una macchina completa nonostante la propria ricchezza, la posizione sociale, i finanziamenti governativi, un decennio di ricerca-e-sviluppo (diremo ora) ed il meglio dell’ingegneria britannica.
Le ragioni sono ancora dibattute e vi sono molte considerazioni da fare:
sono tutti fattori da tenere in considerazione.
Babbage era un personaggio di grande principio ma facilmente offendibile e incline a forti critiche pubbliche da parte di coloro che considerava suoi nemici.
Babbage era anche un pessimo “marketer” di sé stesso, dei suoi progetti. Disdegnava di tenere conferenze sul suo lavoro e non proclamava né promuoveva il potenziale matematico delle sue macchine. Di conseguenza esse sono state giudicate soprattutto per la loro “utilità pratica” per produrre tabelle prive di errori, e gli esperti dell’epoca non erano d’accordo sul fatto che ci fosse una reale necessità di nuove tabelle con altissima precisione: alcuni sostenevano che le tabelle esistenti fossero già sufficientemente accurate e che non vi fosse alcuna giustificazione economica per i grandi costi di capitale per la costruzione delle sue enormi macchine. Altri si chiedevano se le venti, trenta o cinquanta cifre di accuratezza su cui insisteva Babbage, fossero giustificate quando le misurazioni potevano essere effettuate con non più di pochi decimali.
Il movimento del XIX secolo per automatizzare il calcolo fallì e il movimento morì in gran parte con Babbage nel 1871. Non c’è una linea continua di sviluppo da Babbage ai tempi attuali, e molti dei principi incorporati nel suo lavoro sono stati reinventati dai pionieri dell’era dell’elettronica, in gran parte nell’ignoranza del suo lavoro. Sebbene la leggenda del suo lavoro non sia mai andata perduta, è stato solo negli anni ’70 che i suoi progetti sono stati studiati in ogni dettaglio e la scala delle sue realizzazioni è emersa più chiaramente.
All’opera di Babbage viene associata quella di colei che viene considerata il primo programmatore informatico Ada Augusta Lovelace A.A.L cui i francesi di CII Honeywell Bull sotto contratto per lo United States Department of Defense (DoD) a fine anni 70 hanno dedicato un nuovo linguaggio di programmazione chiamato appunto ADA.
Approfondimenti
Antonio PiovesanRedazione: [email protected]
© Copyright RED HOT CYBER. PIVA 16821691009
